Pulling the Radius of Gyration with GROMACS
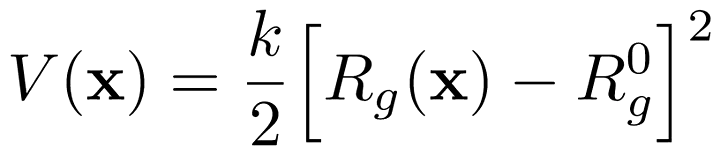
We have written a GROMACS extension that allows you to apply a harmonic (or umbrella-like) restraint along the radius of gyration $R_g$ of a group of atoms (typically molecule).
This can be used for non-equilibrium pulling along $R_g$, or to simply restrain the system along $R_g$.
g_wham coming with this code can read the tpr and pullf.xvg files, so computing a PMF with umbrella sampling should work. Constraints along $R_g$ are not implemented. The source code is an extension of a 4.68 development version of GROMACS, and it is available here:
For compiling the code, please follow the instructions on the GROMACS website for compiling 4.6 versions.
Please note: This comes without any warranty of any kind. We tested the code for a number of cases, and it seems to work fine. In particular, we tested that the width of the histograms along $R_g$ during an umbrella simulation is correct, suggesting that the force calculations are correct. But please test the code carefully for your purpose.
The code implements two new pull geometries, namely pull-geometry = radius-of-gyration or radius-of-gyration1, to be specified in the .mdp file. The first, pull-geometry = radius-of-gyration, indicates pulling along the normal $R_g$, given by
$$ {R_g}^2 = M^{-1} \Sigma_i m_i (\textbf{r}_i - \textbf{R}_s)^2, $$
where $M = \Sigma_i m_i$ is the total mass, and $R_s = M^{-1} \Sigma_i m_i r_i$ is the center of mass. With radius-of-gyration1, the system is instead pulled along
$$ R_g(1) = M^{-1} \Sigma_i m_i |r_i - R_s|. $$
The motivation behind the $R_g^{(1)}$ coordinate is the following: When pulling along the normal $R_g$, the forces applied to the atoms increases with the distance of the atom from the center of mass. You see this easily when taking the derivative of $R_g$ wrt. to the atomic coordinates. Depending on your system, this may be undesirable. When pulling along the $R_g^{(1)}$ coordinate, in contrast, the force on the atoms does not depend on the distance from the center of mass.
The dimensions from which the radius of gyration is computed (x, y, and/or z) is given via the .mdp option pull-dim. For instance, for the $R_g$ around the z-axis, use pull-dim = Y Y N (meaning that only the x- and y-coordinates are used to compute $R_g$). The normal radius of gyration is obtained with pull-dim = Y Y Y.
Not surprisingly, specify the atoms used to compute $R_g$ as pull-group1 (or pull-group2 etc.). Make sure to choose a good PBC atom with pull_pbcatom1, such that the PBC atom is near the center of mass of the pull group. Otherwise, the pull code might not be able to make the group of atoms whole, leading to a sudden jump of the calculated $R_g$ and possibly to huge pull forces. The pull options for the force constant, pulling speed, and initial positions work as usual. No B-states (for free-energy perturbation) are supported.
Output: The pullf.xvg writes as usual the force along the reaction coordinate. This can be used with g_wham -if for computing PMFs. The pullx.xvg shows the center of mass and (as the last column) the reaction coordinate. Use xmgrace -nxy to see $R_g$.
We do not have a reference to cite this code. Maybe you find another paper by us that could be relevant for your work? If not, feel free to use the code, and please mention in your paper that you took the source code from our website. However, please understand that we do not maintain the code or offer other kind of support. If you find a bug, we’ll be happy about a note, but please don’t expect that we fix bugs on short notice. We just hope that the code is useful for someone in our community.