Abstract
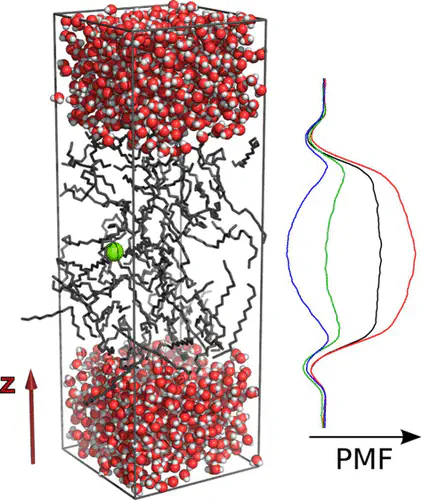
Ewald summation, which has become the de facto standard for computing electrostatic interactions in biomolecular simulations, formally requires that the simulation box is neutral. For non-neutral systems, the Ewald algorithm implicitly introduces a uniform background charge distribution that effectively neutralizes the simulation box. Because a uniform distribution of counter charges typically deviates from the spatial distribution of counterions in real systems, artifacts may arise, in particular in systems with an inhomogeneous dielectric constant. Here, we derive an analytical expression for the effect of using an implicit background charge instead of explicit counterions, on the chemical potential of ions in heterogeneous systems, which (i) provides a quantitative criterium for deciding if the background charge offers an acceptable trade-off between artifacts arising from sampling problems and artifacts arising from the homogeneous background charge distribution, and (ii) can be used to correct this artifact in certain cases. Our model quantifies the artifact in terms of the difference in charge density between the non-neutral system with a uniform neutralizing background charge and the real neutral system with a physically correct distribution of explicit counterions. We show that for inhomogeneous systems, such as proteins and membranes in water, the artifact manifests itself by an overstabilization of ions inside the lower dielectric by tens to even hundreds kilojoules per mole. We have tested the accuracy of our model in molecular dynamics simulations and found that the error in the calculated free energy for moving a test charge from water into hexadecane, at different net charges of the system and different simulation box sizes, is correctly predicted by the model. The calculations further confirm that the incorrect distribution of counter charges in the simulation box is solely responsible for the errors in the PMFs.