g_wham — A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates
Abstract
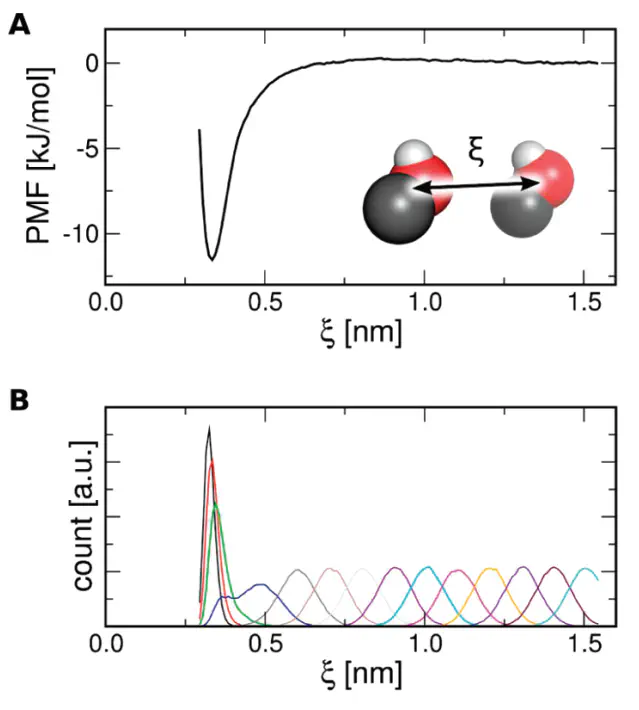
The Weighted Histogram Analysis Method (WHAM) is a standard technique used to compute potentials of mean force (PMFs) from a set of umbrella sampling simulations. Here, we present a new WHAM implementation, termed g_wham, which is distributed freely with the GROMACS molecular simulation suite. g_wham estimates statistical errors using the technique of bootstrap analysis. Three bootstrap methods are supported: (i) bootstrapping new trajectories based on the umbrella histograms, (ii) bootstrapping of complete histograms, and (iii) Bayesian bootstrapping of complete histograms, that is, bootstrapping via the assignment of random weights to the histograms. Because methods ii and iii consider only complete histograms as independent data points, these methods do not require the accurate calculation of autocorrelation times. We demonstrate that, given sufficient sampling, bootstrapping new trajectories allows for an accurate error estimate. In the presence of long autocorrelations, however, (Bayesian) bootstrapping of complete histograms yields a more reliable error estimate, whereas bootstrapping of new trajectories may underestimate the error. In addition, we emphasize that the incorporation of autocorrelations into WHAM reduces the bias from limited sampling, in particular, when computing periodic PMFs in inhomogeneous systems such as solvated lipid membranes or protein channels.